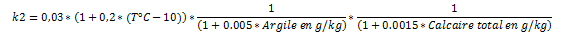L'Agro-calculette K2 : Différence entre versions
(Page créée avec « {{#css:/pages/css/styles_Outils4.css}} == Agrocalculette de calcul du k2 et des pertes annuelles en matière organique == === Estimation du coefficient k2 === <div id="... ») |
|||
| (9 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | |||
== Agrocalculette de calcul du k2 et des pertes annuelles en matière organique == | == Agrocalculette de calcul du k2 et des pertes annuelles en matière organique == | ||
| + | |||
| + | ''La minéralisation est le passage du monde organique au monde minéral, elle est symbolisée par le k2 de la matière organique .'' | ||
| + | ''Aujourd’hui différents modèles existent pour simuler à la fois la minéralisation primaire des matières organiques jeunes et la minéralisation secondaire des produits stables (humus).'' | ||
| + | |||
| + | '''La valeur de k2 dépend des principaux paramètres qui peuvent influencer la minéralisation du carbone du sol :''' | ||
| + | |||
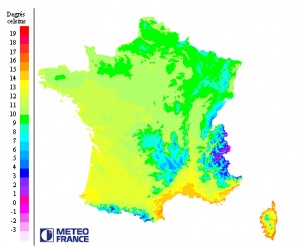
| + | • La température moyenne annuelle, en augmentant, accélère la minéralisation (pour la gamme des valeurs habituelles) ; | ||
| + | |||
| + | • La présence de calcaire total va ralentir la minéralisation de la matière organique du sol ; | ||
| + | |||
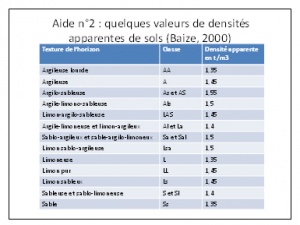
| + | • La teneur en argile et les qualités des argiles augmentent le temps de résidence du carbone ; | ||
| + | |||
| + | • Le pH est un paramètre aussi très important : trop acide, la matière organique s’accumule et le taux de minéralisation est réduit. | ||
| + | |||
| + | |||
| + | '''AUREA vous propose d’évaluer le taux de minéralisation de la matière organique et les pertes annuelles de MO d’un sol, à partir de données simples d’une analyse de terre. Deux formules sont proposées. Elles correspondent à celles qui sont appliquées par AUREA :''' | ||
| + | |||
| + | * <span style="color:#336699 ">Formule adaptée de Rémy & Marin-Laflêche (1976)</span>, utilisable dans toutes les situations (mais calibrée au départ pour le Nord de la France). Elle se base sur les teneurs en argile, en calcaire total et sur la valeur du pHeau. | ||
| + | |||
| + | * <span style="color:#336699 ">Formule actualisée, utilisée en Languedoc-Roussillon , d’après Girard et al (2011)</span> La formule est la suivante :[[Fichier:wikiavril-image2.jpg]] | ||
| + | |||
| + | {{#css:/pages/css/styles_Outils4.css}} | ||
| + | [[Image:aide1.jpeg|vignette|frameless|right|Aide 1]] | ||
| + | [[Image:aide2.jpeg|vignette|frameless|right|Aide 2]] | ||
=== Estimation du coefficient k2 === | === Estimation du coefficient k2 === | ||
Version actuelle en date du 20 juillet 2016 à 11:18
Agrocalculette de calcul du k2 et des pertes annuelles en matière organique
La minéralisation est le passage du monde organique au monde minéral, elle est symbolisée par le k2 de la matière organique . Aujourd’hui différents modèles existent pour simuler à la fois la minéralisation primaire des matières organiques jeunes et la minéralisation secondaire des produits stables (humus).
La valeur de k2 dépend des principaux paramètres qui peuvent influencer la minéralisation du carbone du sol :
• La température moyenne annuelle, en augmentant, accélère la minéralisation (pour la gamme des valeurs habituelles) ;
• La présence de calcaire total va ralentir la minéralisation de la matière organique du sol ;
• La teneur en argile et les qualités des argiles augmentent le temps de résidence du carbone ;
• Le pH est un paramètre aussi très important : trop acide, la matière organique s’accumule et le taux de minéralisation est réduit.
AUREA vous propose d’évaluer le taux de minéralisation de la matière organique et les pertes annuelles de MO d’un sol, à partir de données simples d’une analyse de terre. Deux formules sont proposées. Elles correspondent à celles qui sont appliquées par AUREA :
- Formule adaptée de Rémy & Marin-Laflêche (1976), utilisable dans toutes les situations (mais calibrée au départ pour le Nord de la France). Elle se base sur les teneurs en argile, en calcaire total et sur la valeur du pHeau.
- Formule actualisée, utilisée en Languedoc-Roussillon , d’après Girard et al (2011) La formule est la suivante :